W teorii Lauego rozpatrywana jest dyfrakcja promieni rentgenowskich na sieci przestrzennej kryształu, przy przyjęciu następujących założeń upraszczających:
- Atomy w krysztale ułożone są według idealnego schematu sieci przestrzennej.
- Atomy są nieruchome, tzn. nie wykonują drgań cieplnych.
- Promieniowanie rentgenowskie padające na kryształ uginane jest przez każdy z atomów, a czynnikiem rozpraszającym promienie rentgenowskie są elektrony.
- Wszystkie elektrony danego atomu w sieci skupione są w jednym punkcie (w węźle sieci przestrzennej), tworząc jakby jedną cząstkę o zdolności rozpraszania promieni rentgenowskich proporcjonalnej do liczby skupionych elektronów.
Promieniowanie rentgenowskie padając na sieć przestrzenną powoduje, że elektrony wykonują drgania w takt drgań pola elektromagnetycznego promieni. Dzięki tym drganiom elektrony stają się źródłem wtórnych fal o długości takiej samej jak długość fali promieniowania padającego. Wtórne fale rozchodzą się kuliście od poszczególnych węzłów sieci przestrzennej, przy czym w pewnych ściśle określonych kierunkach kuliste fale wtórne w wyniku interferencji ulegają wzmocnieniu, co doprowadza do powstawania tzw. wzmocnionych promieni interferencyjnych. Promienie te w doświadczeniach obserwujemy jako promienie ugięte, tzn. odchylone od kierunku wiązki promieni padających. Dyfrakcja polega, więc na interferencyjnym wzmacnianiu promieniowania rozproszonego.
Aby nastąpiło interferencyjne wzmocnienie promieni rozproszonych różnica dróg między promieniami rozproszonymi na sąsiednich węzłach prostej sieciowej musi być równa całkowitej wielokrotności długości fali, czyli
∆S=Hλ,
gdzie H – liczba całkowita (określająca rząd ugięcia), λ- długość fali promieniowania.
Ponieważ AC=acosα, DB=acosαo więc:
∆S=Hλ = a(cosα
- cosα)
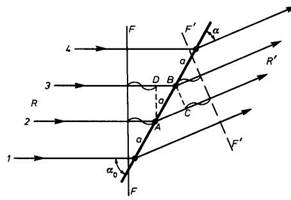 |
Obraz dyfrakcyjny prostej sieciowej na która pada wiązka promieniowania równoległych promieni rentgenowskich pod kątem αo =90° składa się z szeregu współosiowych stożków, na pobocznicach których leżą wzmocnione promienie interferencyjne. Przy założeniu stałości kąta αo, periodu identyczności a oraz H, przy λ =const równanie sprowadza się do postaci α=const. Geometrycznym obrazem funkcji α =const jest stożek, którego osią jest rozważana prosta sieciowa, a tworząca nachylona jest do prostej pod kątem α. Promienie ugięte na prostej sieciowej nie leżą wyłącznie w płaszczyźnie rysunku, lecz układają się na pobocznicach stożków (o kątach rozwarcia 2α, niejednakowych dla różnych różnic dróg), przy czym stożki zwrócone są podstawami zarówno ku dołowi jak i ku górze. Stożki noszą nazwę stożków interferencyjnych (i są odpowiednio stożkami 0, 1, ,2 ,3... H-tego rzędu ugięcia).
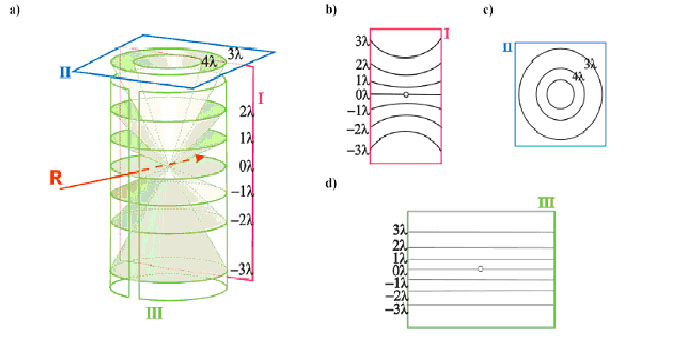 Różne możliwości ustawienia błony fotograficznej w celu rejestracji obrazu dyfrakcyjnego prostej sieciowej; 0λ, 1λ, 2λ... – rząd ugięcia (a) i schematy zarejestrowanych obrazów (b, c, d). R – wiązka pierwotna promieni |
Sieć przestrzenną można traktować jako układ trzech, różnie w trójwymiarowej przestrzeni zorientowanych zbiorów prostych sieciowych, przy czym w każdym zbiorze wszystkie proste sieciowe są do siebie równoległe. Jeżeli na taki układ pada polichromatyczna wiązka monochromatycznych promieni, to kierunek każdego powstającego promienia interferencyjnego określony jest dla danej sieci przestrzennej i dla danej długości fali
trzema równaniami Lauego:
|
a (cos α - cos αo)=H λ b
(cosβ - cosβo)=K λ
c
(cosγ - cosγo)=L λ
gdzie H, K, L określają rząd interferencji. a, b, c – period identyczności wzdłuż prostych sieciowych X, Y, Z. Kąty β, βo, γ, γo analogicznie jak w przypadku prostej sieciowej X. |
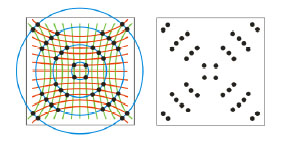
Wzmocniony promień interferencyjny powstaje gdy jednocześnie dla tej samej długości fali są spełnione 3 równania Lauego. Wówczas stożki dyfrakcyjne przecinają się wzdłuż jednej prostej. Prosta ta wyznacza kierunek rozchodzenia się promieniowania ugiętego. Jeżeli błonę fotograficzną umieści się prostopadle do jednej z osi krystalograficznych to - gdy osie X, Y, Z są wzajemnie prostopadłe – zarejestrowany na tej błonie obraz dyfrakcyjny powstały w wyniku nałożenia na siebie dwóch układów hiperboli i jednego układu koncentrycznych kół bezie wyglądał jak poniżej. Na błonie fotograficznej będą zaczernione tylko te punkty, w których przecinają się krzywe.
 |