Sieć odwrotna jest abstrakcyjnym tworem geometrycznym, sprzężonym przestrzennie i wymiarowo z siecią rzeczywistą (krystaliczną). Parametrami komórki elementarnej sieci odwrotnej są a0*, b0*, c0*, α*, β*, γ*.
Aby skonstruować sieć odwrotną należy wybrać jej punkt początkowy w dowolnym miejscu sieci rzeczywistej i następnie poprowadzić normalne do każdej rodziny płaszczyzn sieciowych. Następnie odkłada się na normalnych (licząc od punktu początkowego) odcinki 1/dhkl. Na ich końcach znajdują się punkty zwane węzłami sieci odwrotnej. Reprezentują one odpowiednie płaszczyzny sieci krystalicznej, o długościach równych odwrotnością odległości międzypłaszczyznowych. Węzły te oznacza się symbolami płaszczyzn, ale bez nawiasów.
Istnieje ścisłe powiązanie nomenklatury i symboliki stosowanej w obu sieciach
np. Jeśli płaszczyzna (100) sieci rzeczywistej jest prostopadła do osi X to tak samo jest w sieci odwrotnej.
Długość wektora sieci odwrotnej prostopadłego do płaszczyzny sieci rzeczywistej (hkl) określa wzór
/r*hkl/ = 1/dhkl
Można następnie wywnioskować, że
/a0*/ = 1/d100 ; /b0*/ = 1/d010 ; /c0*/ = 1/d001.
Długość wektora sieci rzeczywistej prostopadłego do płaszczyzny sieci odwrotnej, oznaczanej symbolem (uvw)*,określa wzór
/tuvw/ = 1/d(uvw)*
Można następnie wywnioskować, że
/a0/ = 1/d(100)* ; /b0/ = 1/d(010)* ; /c0/ = 1/d(001)*.
Sieć odwrotna pozwala na geometryczną interpretację warunku dyfrakcji.
W tym celu równanie Lauego zastępuje się jednym równaniem wektorowym, w którym wiązkę padającą i ugiętą oznaczamy symbolami k i k0 o długościach równych 1/ λ .
Wówczas równanie Lauego przybiera postać
|
(λ-1cosα
- λ-1cosα0)a0
= h
|
Równanie Lauego jest równoznaczne z równaniem Bragga więc
|
/r*/ = 1/d.
|
Ze względu na to, że kąt między wektorami k i k0 to kąt ugięcia 2θ to
|
2sinθ/λ = 1/d
|
czyli
|
2dsinθ = λ
|
Wektorowe równanie Lauego pozwala na prostą, geometryczną interpretację warunków dyfrakcji zwaną konstrukcją Ewalda. Jeżeli początki wektorów wiązek umieścimy w jednym punkcie (np. punkt padania promieniowania na kryształ), to końce wektorów falowych wszystkich wiązek ugiętychbędą leżały na powierzchni kuli o promieniu 1/ λ zwanej
sferą Ewalda.
Gdy na sferę nałożymy sieć odwrotną tak, aby jej początek znajdował się w punkcie przebicia sfery przez koniec wektora wiązki padającej, to dyfrakcja zajdzie wówczas, gdy jakiś węzeł sieci odwrotnej znajdzie się na sferze.
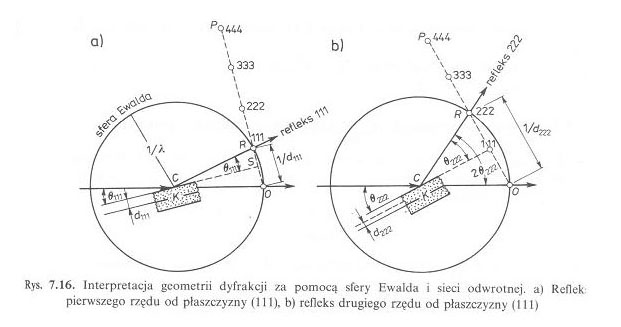 |